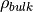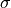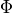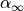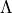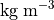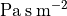Material Parameter Determination

The main use of the infinite-layer classes is the design and simulation of acoustic treatment. Before this can be done the correct parameters of the desired materials are required.

Symbol	Constructor argument	Description
$\rho_{bulk}$	rho_bulk	Density of absorber matrix and fluid
$\sigma$	flow_res	static air flow resistivity
$\Phi$	porosity	volume porosity
$\alpha_\infty$	tortuosity	tortuosity
$\Lambda$	length_visc	viscous characteristic length
$\Lambda'$	length_therm	thermal characteristic length
limp or rigid model	limp	switch

For this purpose a large and expensive set of test requirements is necessary. The first three parameters are usually directly measured parameters but the last three are derived by inverse methods, e.g. by parameter fitting of test to simulation results. One option is described in [Ata2005] and is based on reducing a cost function that is the sum of squared differences of the measured and simulated surface impedance .

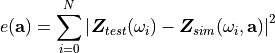
(1) $e({\bf a}) = \sum_{i=0}^N \left|\boldsymbol{Z}_{test}(\omega_i)-\boldsymbol{Z}_{sim}(\omega_i,{\bf a})\right|^2$

where 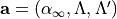${\bf a} = (\alpha_\infty,\Lambda,\Lambda')$ was determined from impedance tube tests in [Ata2005]. However, even more variables can be derived by Atallas method, but one should keep in mind that the sensitity to errors is getting larger the more parameters are derived form the minimisation of the costfunction.

The SciPy package provides many methods for curve fitting and minimisation. Thus, pyva in combination with the capabilities of scipy is an ideal toolset for this task.

Atalla Test Case

The following inputs are required:

# Numerics
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import dual_annealing

# pyva packages
import pyva.properties.materialClasses as matC
import pyva.models as mds
import pyva.systems.infiniteLayers as iL

Three parameters are derived by direct test methods:

Symbol	Fibrous1	Unit
$\rho_{bulk}$	89.6	${\rm kg\:m}^{-3}$
$\sigma$	21235	${\rm Pa\:s\:m}^{-2}$
$\Phi$	0.94

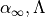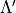The remaining parameters $\alpha_\infty, \Lambda$ and $\Lambda'$ must be determined by minimizing (1) So we define the given parameters with:

# Fibrous 1
flow_res = 21235.
porosity = 0.94
rho_bulk = 89.6

Further important test parameters are the thickness of the specimen and the environmental conditions:

h = 23.37e-3
T = 22.6+273.15
P0 = 1.002

These conditions are applied by using the air() method:

air_test = matC.Fluid.air(T,P0)

The first step is to create a function that gives an EquivalentFluid with these three parameters as input:

def fibre_fit(tor,Lam_visc,Lam_term):
    return matC.EquivalentFluid(flow_res, porosity , tor, rho_bulk, \
                              Lam_visc, Lam_term,\
                              rho0 = air_test.rho0, \
                              c0 = air_test.c0,\
                              dynamic_viscosity = air_test.dynamic_viscosity,\
                              Cp = air_test.Cp, heat_conductivity=air_test.heat_conductivity, \
                              limp = limp )

in a second step, this function is used to create TMmodel of the set-up:

def layer_fit(tor,Lam_visc,Lam_term):
    return mds.TMmodel((iL.FluidLayer(h,fibre_fit(tor,Lam_visc,Lam_term)),))

and third, to create the surface impedance of this:

def impedance_fit(f,tor,Lam_visc,Lam_term):
    return layer_fit(tor,Lam_visc,Lam_term).impedance(2*np.pi*f,0.).ydata.flatten()

For the cost function the test data is required that the author has tried to derive graphically from the original paper. It is imported by

# Import test data
f_test,Zs_re,Zs_im = np.loadtxt ('.//data//'+test_str[test-1]+'.csv',
                    unpack = True,
                    usecols = (0,1,2), skiprows = 1,
                    delimiter = ',')

# create absolute values
Zs = (Zs_re+1j*Zs_im)*z0

According to [Ata2005] only values above 500 Hz are considered due to low precision below this limit.

# index for frequency range selection
i_freq = f_test >= f_min

We are now prepared to create the cost function:

def cost_function(x):
    return np.sum(np.abs(impedance_fit(f_test[i_freq],x[0],x[1],x[2])-Zs[i_freq])**2)

Lower and upper bound are required and chosen according to [Ata2005]:

# set bounds
lw = [1.,1.e-6,1.e-6] # lower bounds
up = [4.,4.e-4,4.e-4] # upper bounds
bounds=list(zip(lw, up))

The dual_annealing method from the scipy.optimize package does the final job for us:

res = dual_annealing(cost_function, bounds = bounds)

With the following result:

>>> res
    fun: 10445.463547490406
 message: ['Maximum number of iteration reached']
    nfev: 6285
    nhev: 0
     nit: 1000
    njev: 71
  status: 0
 success: True
       x: array([1.00000000e+00, 3.48187655e-05, 1.51283590e-04])

By using the impedance_fit function with this parameters we get the result in terms of the surface impedance

z_surf = impedance_fit(freq, *res.x)

In figure Surface impedance of fibrous material. Pyva and [Ata2005] Results. the result of such a set-up is shown and compared to the results received with parameters from [Ata2005]. We see that the author did not perfectly succeed in picking the data from the paper copy. However, the general option to receive the parameters from impedance tests without expensive commercial software and using pyva, python and some powerful toolboxes is demonstrated.

Further materials from [Ata2005] can be tested with the full example in Material Parameter Determination. If you interested in applying the method on your test data, feel free to contact the author at author@alexanderpeiffer.de. Test impedance data with additional parameters derived by other methods are very welcome.

_images/atalla_JCA_parameter_fibrous1.png — Surface impedance of fibrous material. Pyva and [Ata2005] Results.