Lumped Models

The lumpedSystems module has only one system implemented, but this is an important one: The harmonic oscillator, the mother system of all vibro-acousticians!

Not really useful in all technical application but helpful for understanding of damping and resonance effects. A simple oscillator is created with:

import pyva.systems.lumpedSystems as lSys

# First example for oscillator
mass   = 0.1
ks     = 98.696 # spring stiffness

# Undamped HO
myHO = lSys.HarmonicOscillator(mass,ks)

With specific initial conditions the motion of the HarmonicOscillator can be calculated by the displacement() method

# evenly sampled time at 200ms intervals
time = np.arange(0., 0.5, 0.001)

# Initial conditions
x0 = 0.1
v0 = 1.4

plt.plot(time, myHO.displacement(time,x0,v0))

Leading to the following graph

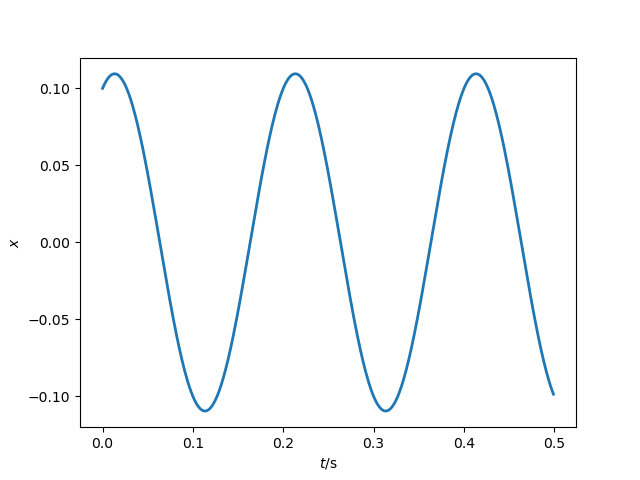
Oscillatory motion of undamped harmonic oscillator.

Interesting damped cases are created using the critical damping as reference constant

# Derive all other constants from this
c_vc   = myHO.critical_viscous_damping

# Damped HOs
cv1  = c_vc*3   # overdamped
cv2  = c_vc/10  # underdamped

myHO_uD = lSys.HarmonicOscillator(mass,ks,cv2)
myHO_oD = lSys.HarmonicOscillator(mass,ks,cv1)
myHO_cD = lSys.HarmonicOscillator(mass,ks,c_vc)

Providing the following plot from

plt.plot(time, myHO_uD.displacement(time,x0,v0),lw=2,label = 'underdamped')
plt.plot(time, myHO_oD.displacement(time,x0,v0),lw=2,label = 'overdamped')
plt.plot(time, myHO_cD.displacement(time,x0,v0),lw=2,label = 'critically damped')

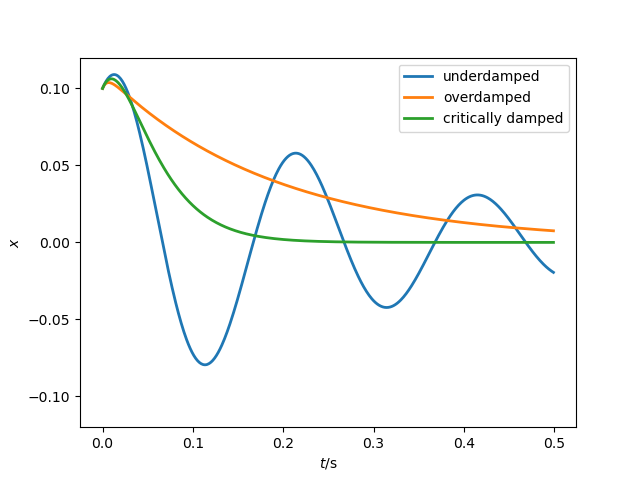
Oscillatory motion of damped harmonic oscillators.

Forced harmonic motion can also be found with the u_force() method

force = 10.0
omega = np.linspace(0,4*myHO.omega_mode,200)

plt.plot(omega, np.abs(myHO_uD.u_force(omega,force)),lw=2,label = 'underdamped')
plt.plot(omega, np.abs(myHO_oD.u_force(omega,force)),lw=2,label = 'overdamped')
plt.plot(omega, np.abs(myHO_cD.u_force(omega,force)),lw=2,label = 'critically damped')

Providing the following amplitude slope over frequency

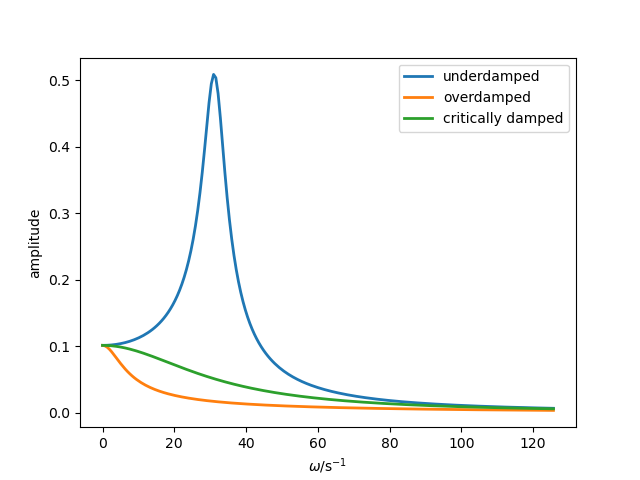
Amplitude over frequency of forced harmonic oscillators with damping.