pyva.coupling.junctions.LineJunction
- class pyva.coupling.junctions.LineJunction(systems, length, thetas)
Bases:
JunctionClass for line junctions
- systems
of systems
- Type:
list or tuple
- length
length of LineJunction
- Type:
float
- thetas
angles of connected plates
- Type:
ndarray
- __init__(systems, length, thetas)
Class contructor for LineJunction.
- Parameters:
systems (list or tuple) – systems connected to junction
length (float) – length of LineJunction
thetas (list or tuple) – angles of connected plates
Methods
CLF(omega[, i_sys, i_in_wave, i_out_wave, ...])coupling loss factor for line junctions
CLF_angle(omega[, i_sys, i_in_wave, ...])coupling loss factor for wave fields of plates
__init__(systems, length, thetas)Class contructor for LineJunction.
get_wave_DOF([ix])Provides the local wave DOFs of the junction
index(ID)Determines index of ID in system list of junction
junction_matrix(omega[, N_step, method])Creates junction matrix for LineJunction (all upper triangular)
kx(omega, i_sys, i_in_wave, i_out_wave, Nstep)wavenumber sampling for diffuse field intgegration.
max_inplane_wavenumber(omega)Determine the maximal in-plane wavenumber of all connected plates
modal_density(omega)Provides modal density
total_radiation_stiffness_wavenumber(omega, ...)Calculates the total radiation stiffness of line junctions
Calculate the total radiation stiffness of line junctions.
transmission_wavenumber(omega, wavenumber[, ...])Calculates the transmission coefficient of line junctions
transmission_wavenumber_LM(omega, wavenumber)Calculate the transmission coefficient of line junctions (LinearMatrix Version).
transmission_wavenumber_diffuse(omega[, ...])Diffuse transmission coefficient for line junctions.
transmission_wavenumber_langley(omega, ...)transmission coefficient based on the wave transionmssion method
transmission_wavenumber_wave(omega, wavenumber)Transmission coefficient assuming wave transformations for radiation stiffness.
Attributes
Number of connected physical SEA systems (not wave_fields)
Number of wave fields
Provides 'excitation' DOFs of junction SEA matrix
Provides input wave dofs of junction for upper triangular input matrix
Provides output wave dofs of junction for upper triangular input matrix
Provides 'response' DOFs of junction SEA matrix
- CLF(omega, i_sys=(0, 1), i_in_wave=(5, 5), i_out_wave=(5, 3), N_step=100, method='diffuse', Signal=True)
coupling loss factor for line junctions
This method calculates the CLF from system i_sys[0] to i_sys[1]. The wavefields that are considered are given by i_in_wave and i_out_wave. The CLF is calculated running through through both indexes
- Parameters:
omega (ndarray or float) – angular frequency.
i_sys (ndarray,list or tuple, optional) – indexes of incident and radiating system. The default is (0,1).
i_in_wave (ndarray,list or tuple, optional) – DESCRIPTION. The default is (5,5).
i_out_wave (ndarray,list or tuple, optional) – DESCRIPTION. The default is (5,3).
N_step (int, optional) – Number of angle integration intervals. The default is 100.
method (str, 'diffuse' or 'langley', optional) – identifier for calculation method. The default is ‘diffuse’.
Signal (bool, optional) – Switch for Signal output. The default is True.
- Raises:
ValueError – For non consistent arguments.
- Returns:
coupling loss factor.
- Return type:
ndarray or Signal
- CLF_angle(omega, i_sys=(0, 1), i_in_wave=(5, 3), i_out_wave=(5, 3), N_step=200, method='diffuse', Signal=True)
coupling loss factor for wave fields of plates
This method uses the transmission_wave_number_diffuse function that is based in angular integration. The normal CLF method uses the wavenumber integration.
Options for i_in/out_wave are 0 : all 1 : longitudinal 2 : shear 3/4 : bending 5 : in-plane (longitudinal + shear)
- Parameters:
omega (np.array) – angular frequency
L (double) – length of junction
i_sys (tupel of integer) – pair of in- and out systems. The default is (0,1), if (0,0) only tau between waves is considered
i_in_wave (TYPE, optional) – wave_fields index of exciting waves. The default is (5,3).
i_out_wave (TYPE, optional) – wave_fields index of outgoing waves. The default is (5,3).
N_step (TYPE, optional) – Number of steps for numerical angle integration. The default is 200.
method (TYPE, optional) – Method of tau calculation. ‘diffuse’ for diffuse reciprocity, ‘langley’ for wave transmission. The default is ‘diffuse’.
- Return type:
Signals with coupling loss factors
- property N
Number of connected physical SEA systems (not wave_fields)
- Returns:
number of systems
- Return type:
int
- property N_wave
Number of wave fields
- Returns:
Number of wave fields
- Return type:
int
- property exc_DOF
Provides ‘excitation’ DOFs of junction SEA matrix
The ‘excitation’ and response DOFs are equal in terms of ID and wave_dof but use ‘power’ as physical input
- Returns:
excitation DOFs of junction SEA matrix
- Return type:
- get_wave_DOF(ix=slice(None, None, None))
Provides the local wave DOFs of the junction
- Returns:
dofs of junction, list of systems
- Return type:
DOF,sys_list
- property in_dofs
Provides input wave dofs of junction for upper triangular input matrix
These DOFs are requiered to determine the column index of the upper triangular components in the global SEA matrix.
For example a plate - cavity junction has wave dofs [ ID=1,dof=3 ; 1,5 ; 2,0 ]
The full of diag CLF in the SEA matrix are
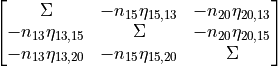
The column dofs would be : [ 1,5 ; 2,0 ; 2,0]
See also
- Returns:
wave_DOF of column.
- Return type:
- index(ID)
Determines index of ID in system list of junction
- Parameters:
ID (int) – System ID
- Returns:
index of ID in system list (-1) if not found
- Return type:
int
- junction_matrix(omega, N_step=200, method='diffuse')
Creates junction matrix for LineJunction (all upper triangular)
This method calculates the all CLF of junction matric [J] The wavefields that are considered ar either the pressure wave or the bending wave The CLF is calculated running through through both indexes
- Parameters:
omega (float) – angular frequency.
N_step (int, optional) – Number of integration steps. The default is 90.
method (str, optional) – CLF calculation method. The default is ‘diffuse’.
- Returns:
JM – JunctionMatrix.
- Return type:
DynamiMatrix
- kx(omega, i_sys, i_in_wave, i_out_wave, Nstep, method='angle')
wavenumber sampling for diffuse field intgegration.
The different wave number regimes require a well balanced sampling of the wavnumber. High sampling in-plane waves and low sampling for bending waves
- Parameters:
omega (double) – angular frequency
i_sys (tupel or list of int) – system index
i_in_wave (tupel or list of int) – wave_DOF of irradiating wave field
i_out_wave (tupel or list of int) – wave_DOF of radiating wave field
Nstep (int) – Integration steps
method (str) – ‘angle’ for angular integration with dense sampling at 90 degrees ‘in-plane’ for two intervals, kx = [0 kS ) + [kS kB)
- Returns:
kx – wavenumber in x
- Return type:
ndarray
- max_inplane_wavenumber(omega)
Determine the maximal in-plane wavenumber of all connected plates
Bending wavenumber can be orders of magnitude higher. In this case the in-plane wave may be undersampled. Thus, for all wavenumber intergration the upper boundary of the in-plane wavenumber is required for better sampling of 0 > kx > kS.
- Parameters:
omega (float) – angular frequency.
- Returns:
k_max – maximal wavenumber.
- Return type:
float
- modal_density(omega)
Provides modal density
Calculates the modal density for all connected wavefields of the junction.
- Parameters:
omega (ndarray) – angular frequency.
- Returns:
res – modal density.
- Return type:
ndarray of dimension N_wave x size(omega)
- property out_dofs
Provides output wave dofs of junction for upper triangular input matrix
These DOFs are requiered to determine the row index of the upper triangular components in the global SEA matrix.
For example a plate - cavity junction has wave dofs [ 1,3 ; 1,5 ; 2,0 ]
The full of diag CLF in the SEA matrix are
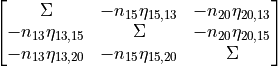
The column dofs would be : [ 1,3 ; 1,3 ; 1,5]
See also
- Returns:
wave_DOF of rows.
- Return type:
- property res_DOF
Provides ‘response’ DOFs of junction SEA matrix
The ‘response’ and excitation DOFs are equal in terms of ID and wave_dof but use ‘energy’ as physical output
- Returns:
response DOFs of junction SEA matrix
- Return type:
- total_radiation_stiffness_wavenumber(omega, wavenumber)
Calculates the total radiation stiffness of line junctions
The result is given in wavenumber domain and global displacement coordinate system
- Parameters:
omega (float) – angular frequency.
wavenumber (ndarray) – wavenumber in x- (edge) direction.
- Returns:
Total stiffness matrix of line junction
- Return type:
nd.array
- total_radiation_stiffness_wavenumber_LM(omega, wavenumber, i_in_sys=-1)
Calculate the total radiation stiffness of line junctions.
The result is given in wavenumber domain and global displacement coordinate system.
_LM identifies the slow LinearMatrix version
In ref [Pei2022] this is Equation (8.129).
- Parameters:
omega (float) – angular frequency.
wavenumber (ndarray) – wavenumber in x- (edge) direction.
- Returns:
Total stiffness matrix of line junction
- Return type:
- transmission_wavenumber(omega, wavenumber, i_sys=(0, 1), i_in_wave=(3, 3), i_out_wave=(5, 5), Signal=True)
Calculates the transmission coefficient of line junctions
This methods applies the hybrid CLF formulation from [1] but using the radiated power calcualted from the wave amplitude as disscussed in the reference.
The rad_sw argument is used for validation. For simulation always use ‘wave’
- Parameters:
omega (float or ndarray) – angular frequency.
wavenumber (float or ndarray) – wavenumber in x- or edge-direction.
i_sys (tuple or list, optional) – incident and radiating system index vector. The default is (0,1).
i_in_wave (tuple or list, optional) – incident wave type. The default is (1,2,3).
i_out_wave (tuple or list, optional) – radiating wave type. The default is (1,2,3).
Signal (bool, optional) – switch for Signal output. The default is True.
- Raises:
ValueError – When input values are not or correct type of not constent.
- Returns:
transmission coefficient for one frequency over wavenumber.
- Return type:
ndarray or Signal
- transmission_wavenumber_LM(omega, wavenumber, i_sys=(0, 1), i_in_wave=(1, 2, 3), i_out_wave=(1, 2, 3), rad_sw='wave', Signal=True)
Calculate the transmission coefficient of line junctions (LinearMatrix Version).
This methods applies the hybrid CLF formulation from [1] but using the radiated power calculated from the wave amplitude as disscussed in the reference.
The method is the version that is used for validation purpose, thus the radiated power can be calculated using the radiation stiffness. As shown in [Pei2022] this is not correct in the wavenumber range [k_L < kx < k_S]
The rad_sw argument is used for exactly this validation. For simulation always use ‘wave’
- Parameters:
omega (float or ndarray) – angular frequency.
wavenumber (float or ndarray) – wavenumber in x- or edge-direction.
i_sys (tuple or list, optional) – incident and radiating system index vector. The default is (0,1).
i_in_wave (tuple or list, optional) – incident wave type. The default is (1,2,3).
i_out_wave (tuple or list, optional) – radiating wave type. The default is (1,2,3).
rad_sw (str, 'wave' or 'im_dir', optional) – identifier for radiated power method. The default is ‘wave’.
Signal (bool, optional) – switch for Signal output. The default is True.
- Raises:
ValueError – When input values are not or correct type of not constent.
- Returns:
transmission coefficient for one frequency over wavenumber.
- Return type:
ndarray or Signal
- transmission_wavenumber_diffuse(omega, i_sys=(0, 1), i_in_wave=(5, 5), i_out_wave=(5, 3), N_step=100, CLF_sw=False, method='diffuse', Signal=True)
Diffuse transmission coefficient for line junctions.
When this method is used for calculating Equation (8.160) we don’t need the diffuse field transmission coeffcient <tau> but the pure wavenumber integral that is NOT divided by k_v^(m). For this purpose a switch in intgrated that sets k_in = 1.
- Parameters:
omega (float or ndarray) – angular frequency.
i_sys (tuple or list, optional) – incident and radiating system index vector. The default is (0,1).
i_in_wave (tuple or list, optional) – incident wave_DOF. The default is (5,5).
i_out_wave (tuple or list, optional) – transmissted wave_DOF. The default is (5,3).
N_step (int, optional) – Number of wavenumber integration steps. The default is 100.
CLF_sw (bool, otional) – Sets the incoming wavenumber to 1 if True for use in line junctin matrix Eq. (8.160). The default is False.
method (str, optional) – Mewthod seclector ‘diffuse’ for diffuse field reciprocity, ‘langley’ for wave transmission. The default is ‘diffuse’.
Signal (bool, optional) – Swith for return datatype. The default is True.
- Returns:
diffuse field transmission coefficient.
- Return type:
ndarray (Signal = False) or Signal
- transmission_wavenumber_langley(omega, wavenumber, i_sys=(0, 1), i_in_wave=(1, 1, 1, 2, 2, 2, 3, 3, 3), i_out_wave=(1, 2, 3, 1, 2, 3, 1, 2, 3), matrix=False, Signal=True)
transmission coefficient based on the wave transionmssion method
The version is based on the wave trasmission theory from [2] The transmission is calculated for each specific wave type, this is not possible for the hybrid CLF as the diffuse field reciprocity is not valid for single in-plane waves.
The matrix argument is for test pupose to check if the analytical expression is correct.
- Parameters:
omega (float or ndarray) – angular frequency.
wavenumber (float or ndarray) – wavenumber in x- or edge-direction.
i_sys (tuple or list, optional) – incident and radiating system index vector. The default is (0,1).
i_in_wave (tuple or list, optional) – incident wave_DOF. The default is (1,1,1,2,2,2,3,3,3).
i_out_wave (tuple or list, optional) – transmissted wave_DOF. The default is (1,2,3)*3.
matrix (bool, optional) – Switch if the matrix D.f - q (True) or the expicity analytical version is used. The default is False.
Signal (TYPE, optional) – DESCRIPTION. The default is True.
- Returns:
transmission coefficient.
- Return type:
ndarray
- transmission_wavenumber_wave(omega, wavenumber, i_sys=(0, 1), i_in_wave=(1, 1, 1, 2, 2, 2, 3, 3, 3), i_out_wave=(1, 2, 3, 1, 2, 3, 1, 2, 3), matrix=False)
Transmission coefficient assuming wave transformations for radiation stiffness.
New try to use the wave amplidute base to allow separate treatment of L,S and B waves.
- Parameters:
omega (TYPE) – DESCRIPTION.
wavenumber (TYPE) – DESCRIPTION.
i_sys (TYPE, optional) – DESCRIPTION. The default is (0,1).
i_in_wave (TYPE, optional) – DESCRIPTION. The default is (1,)*3+(2,)*3+(3,)*3.
i_out_wave (TYPE, optional) – DESCRIPTION. The default is (1,2,3)*3.
matrix (TYPE, optional) – DESCRIPTION. The default is False.
- Return type:
None.